查找树

二叉排序树

  二叉排序树是一棵具有如下特征的二叉树

1. 若左子树非空，则左子树上所有结点的值均小于根结点的值
2. 若右子树非空，则右子树上所有结点的值均大于根结点的值
3. 左右子树分别是一棵二叉排序树

如下二叉排序树，依次插入了5、3、7、1、4、2

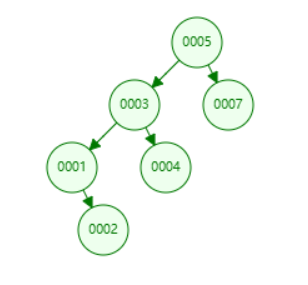
  向二叉排序树中插入元素时，应符合如下规则

1. 若原二叉排序树为空，则直接插入
2. 原二叉排序树不为空，若待插入关键字小于结点值，则插入到左子树，大于结点值，则插入到右子树

  删除元素时，应符合如下规则

1. 若被删除的结点是叶节点，则直接删除
2. 若被删除的结点只有一棵左子树或右子树，则让被删除结点的子树顶替被删除的结点
3. 若被删除的结点同时拥有左右子树，则让二叉排序树在中序遍历下，被删除结点的直接后继顶替被删除的结点

平衡二叉树

  在二叉排序树的基础下，确保任意结点的左右子树高度相差不超过1，如下平衡二叉树，依次插入了5、3、7、1、4、2

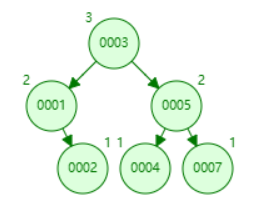
  向平衡二叉树中插入元素后，若导致二叉树不平衡，先找到离插入结点最近的不平衡二叉树的根结点，对该根结点做出相应调整

1. LL平衡旋转：右旋
2. RR平衡旋转：左旋
3. LR平衡旋转：左旋+右旋
4. RL平衡旋转：右旋+左旋

  在平衡二叉树中删除元素后，若导致二叉树不平衡，先找到离插入结点最近的不平衡二叉树的根结点，对该根结点做出相应调整

1. LL平衡旋转：右旋
2. RR平衡旋转：左旋
3. LR平衡旋转：左旋+右旋
4. RL平衡旋转：右旋+左旋

红黑树

  在二叉排序树的基础下，满足如下性质

1. 每个结点或是红色，或是黑色
2. 根结点是黑色的
3. 虚构的外部结点是黑色的
4. 不存在两个相邻的红结点
5. 对每个结点，从该结点到任意一个叶结点的简单路径上，所含黑节点的数量相同

  由红黑树性质得出的三个结论

1. 从根结点到叶结点的最长路径不大于最短路径的2倍
2. 有 $n$ 个内部节点的红黑树的高度 $h \le 2log_2(n+1)$
3. 新插入红黑树的结点初始为红色

  红黑树的插入用二叉查找树插入法插入，初始时将结点 $z$ 着为红色

1. 若结点 $z$ 是根结点，则将结点 $z$ 着为黑色
2. 若结点 $z$ 不是根结点，且结点 $z$ 的父结点是黑色，无需做任何调整
3. 若结点 $z$ 不是根结点，且结点 $z$ 的父结点是红色，分如下三种情况，对红黑树做出不同调整

情况一：结点 $z$ 的叔结点（包括叔结点是外部节点的情况）是黑色的，且结点 $z$ 是一个右孩子，先来一次左旋，再来一次右旋

情况二：结点 $z$ 的叔结点（包括叔结点是外部节点的情况）是黑色的，且结点 $z$ 是一个左孩子，一次右旋

情况三：结点 $z$ 的叔结点（包括叔结点是外部节点的情况）和父结点都是红色的，先将父结点和叔结点着为黑色，爷结点着为红色，再把爷结点做为新结点重复循环

  红黑树的删除用二叉查找树删除方法删除，初始时将结点 $z$ 着为红色

  删除太难了，不写了